'Algorithm'에 해당되는 글 6건

퀵 정렬

 퀵 정렬은 평균적으로 가장 좋은 성능을 가져 현장에서 가장 많이 쓰는 정렬 알고리즘이다. 

정렬 방식

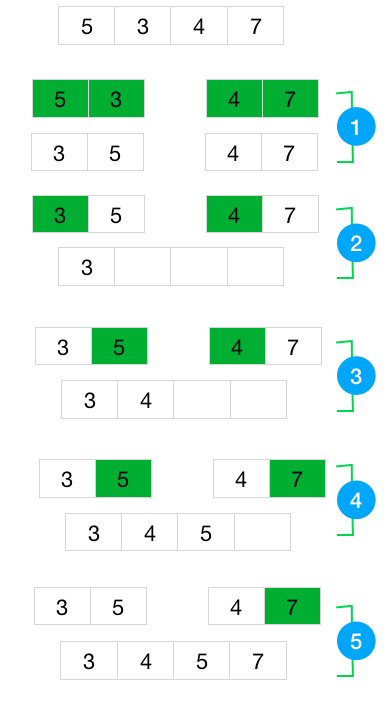
 정렬할 배열에서 "기준원소"를 하나 고른다. 아무 원소나 임의로 골라도 되나 여기서는 맨 뒤의 원소를 기준원소로 삼기로 한다. 이 기준원소를 중심으로 더 작거나 같은 수는 왼쪽으로, 큰 수는 오른쪽으로 재배치한다. 기준원소는 이렇게 분할된 양쪽 부분 배열 사이에 자리하게 된다. 이렇게 분할된 왼쪽 부분 배열을 따로 정렬한다. 마찬가지로 오른쪽 부분 배열도 따로 정렬한다. 기준원소는 손대지 말고 제자리에 그대로 둔다. 기준원소의 왼쪽에 기준원소보다 작은 원소들이 정렬되어 있고, 오른쪽에 기준원소보다 큰 원소들이 정렬되어 있으면 전체 배열은 정렬된 것이다. 여기서 왼쪽과 오른쪽 부분 배열을 정렬할 때 퀵 정렬을 재귀적으로 사용한다. 

퀵 정렬 구현

public class QuickSort {

	private static void quickSort(int[] arr) {
        quickSort(arr, 0, arr.length - 1);
    }

    private static void quickSort(int[] arr, int start, int end) {
        int part2 = partition(arr, start, end);
        if (start < part2 - 1) {
            quickSort(arr, start, part2 - 1);
        }
        if (part2 < end) {
            quickSort(arr, part2, end);
        }
    }

    private static int partition(int[] arr, int start, int end) {
        int pivot = arr[(start + end) / 2]; // 중간값으로 pivot 설정하는 경우
        while (start <= end) {
            while (arr[start] < pivot) start++;
            while (arr[end] > pivot) end--;
            if (start <= end) {
                swap(arr, start, end);
                start++;
                end--;
            }
        }
        return start;
    }

    private static void swap(int[] arr, int start, int end) {
        int tmp = arr[start];
        arr[start] = arr[end];
        arr[end] = tmp;
    }
}

병합 정렬

  병합 정렬은 먼저 입력을 반으로 나눈다. 이렇게 나눈 전반부와 후반부를 각각 독립적으로 정렬한다. 마지막으로 정렬된 두 부분을 합쳐서, 즉 병합하여 정렬된 배열을 얻는다. 여기서 전반부를 정렬할 때도 역시 반으로 나눈 다음 정렬해서 병합한다. 즉, 원래의 정렬 문제와 성격이 똑같고 단지 크기만 반으로 줄었을 뿐이다. 후반부에 대한 정렬도 마찬가지다. 병합 정렬은 자신에 비해 크기가 반인 문제를 두 개 푼 다음, 이들을 병합하는 일을 재귀적으로 반복한다. 

병합 정렬 구현

public class MergeSort {

    public static void main(String[] args) {
        int[] arrays = {6, 3, 1, 21};
        mergeSort(arrays, 0, arrays.length - 1);
    }

    private static void mergeSort(int[] arrays, int p, int r) {
        if (p < r) {
            int mid = (p + r) / 2;
            mergeSort(arrays, p, mid);
            mergeSort(arrays, mid + 1, r);
            merge(arrays, p, mid, r);
        }
    }

    private static void merge(int[] arrays, int p, int mid, int r) {
        int i = p;
        int j = mid + 1;
        int k = p;
        int[] temp = new int[arrays.length];
        while (i <= mid && j <= r) {
            if (arrays[i] < arrays[j]) {
                temp[k++] = arrays[i++];
            } else {
                temp[k++] = arrays[j++];
            }
        }
        while (i <= mid)
            temp[k++] = arrays[i++];
        while (j <= r)
            temp[k++] = arrays[j++];
        for (int index = p; index < k; index++) {
            arrays[index] = temp[index];
        }
    }
}

삽입 정렬

  삽입 정렬은 이미 정렬되어 있는 i개짜리 배열에 하나의 원소를 더 더하여 정렬된 i+1 개짜리 배열을 만드는 과정을 반복한다.

O(n제곱) 시간이 드는 비효율적인 정렬 알고리즘군에 속하지만 배열이 거의 정렬되어 있는 상태로 입력되는 경우에는 가장 매력적인 알고리즘이 된다. 이유는  현재 값이 이전 값보다 작을 경우를 찾는 반복문이 거의 실행되지 않기 때문이다. 

삽입 정렬 구현

public class InsertionSort {

    public static void main(String[] args) {
        int[] arrays = {5, 3, 4, 7, 6, 2, 1};

        int newItem;
        int loc;

        for (int i = 1; i < arrays.length; i++) {
            newItem = arrays[i];
            loc = i;
            while (loc > 0 && newItem < arrays[loc - 1]) {
                arrays[loc] = arrays[loc - 1];
                loc--;
            }
            arrays[loc] = newItem;
        }
    }
}

버블 정렬

  버블 정렬은 선택 정렬처럼 제일 큰 원소를 끝자리로 옮기는 작업을 반복한다.

단 선택 정렬이 가장 큰 수를 찾은 다음 맨 오른쪽 수와 바꾸는 반면, 버블 정렬은 왼쪽부터 이웃한 수를 비교하면서 순서가 제대로 되어있지 않으면 하나하나 바꾸어나간다. 

버블 정렬 구현

public class BubbleSort {
    public static void main(String[] args) {
        int[] arrays = new int[]{8, 31, 48, 73, 3, 65, 20, 29, 11, 15};
        int temp;
        int size = arrays.length;

        for (int i = 0; i < size; i++) {
            for (int j = 0; j < size - 1 - i; j++) {
                if (arrays[j] > arrays[j + 1]) {
                    temp = arrays[j];
                    arrays[j] = arrays[j + 1];
                    arrays[j + 1] = temp;
                }
            }
        }
    }
}